К апериодическим звеньям относится цепочка RC, показанная на рис. 6.16. Здесь напряжение на конденсаторе не может измениться скачком при подаче UBX скачком.

Ток заряда конденсатора зависит от емкости конденсатора С и от скорости изменения напряжения на нем, т. е.

l = C-, (6.18)

ГДе с= вых-

С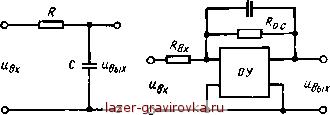

Рис. 6.16. Рис. 6.17.

Уравнение электрического равновесия в данном случае будет иметь следующий вид:

UiR + uc. (6.19)

Подставляя в (6.19) значение i нз (6.18) н учитывая, что с= вых, получаем:

вы* + Г^р-£/вх, (6.20)

где T=RC - постоянная времени.

Как видно, и в данном примере уравнение (6.20) соответствует (6.15) приА=1.

Двигатель постоянного тока с независимым возбуждением прн пуске вхолостую и неучете индуктивности якорной цепи также описывается уравнением, соответствующим апериодическому звену. Действительно, если в уравнение электрического равновесия якорной цепн при питании от вентильного преобразователя

еа = £Фсо -Ь iR0, (6.21)

подставить i ~ j~~> что следует нз уравнения движения

электропривода при холостом ходе [см. (6.37)], получим после преобразований

о>+7 = , (6.22)

где 7ы=Ло/(АФ)3 - электромеханическая постоянная времени, с; / - момент инерции двигателя и всех инерционных масс привода, кг-м2; £Д=1/(£Ф) - коэффициент передачи.

Примером апериодического звена может служить также операционный усилитель, у которого параллельно резистору обратной связи R0 с включается конденсатор С, как это показано на рнс. 6.17. Так как ток h, протекающий через резистор R0.a,

а ток *2, протекающий через конденсатор,

то с учетом, что коэффициент передачи усилителя в разомкнутом состоянии очень велик, получим:

вд ЦВЫХ Q < ВЫХ Q £g

Из (6.23) следует:

ВЫХ 1 * - кивх

гдеГ = /?0>сС; k= RQJRVX.

В результате получилось, что выходное и входное напряжения в схеме иа рис. 6.17 связаны соотношением, аналогичным (6.15), описывающим апериодическое звено.

Уравнения вида (6.15) называются дифференциальными. В теории автоматического регулирования широко используется так называемый операторный метод записи и решения дифференциальных уравнений. При этом вместо dx/dt применяют запись рХ{р), а вместо х - обозначениеХ(р).

Тогда уравнение (6.15) в оперативной форме будет иметь вид:

хвых (р) + тРхт (р) = ftxBX ср). (6.24)

Рис. 6.18.

Отношение вЬГХ называется передаточной функ-хъх (Р)

цией. Из (6.24) следует, что передаточная функция апериодического звена имеет вид:

*вы* tP), -J-. (6.25)

Все рассмотренные звенья, описываемые уравнениями, соответствующими апериодическому звену, имеют

одну и ту же передаточную функцию (6.25). В каждом конкретном случае будут отличаться лишь значения коэффициента к и постоянной времени Т.

Следует отметить, что гиристорный преобразова-ъатель во многих случаях может также рассматриваться как апериодическое звено, т. е.

где kn и Тп - коэффициент усиления и постоянная времени тнристорного преобразователя.

Отметим, что убыстрение (форсировка) процесса изменения напряжения на выходе апериодического звена достигается путем подачи на вход звена повышенного напряжения UBX (рис. 6.15). При той же постоянной времени Т напряжение uRvtx нарастает до значения £/Вых.уст за время Aj><C (3-=-4) Т. Чтобы прн этом сохранить прежнее установившееся значение Овых.ует, нужно в момент времени /ф снять форсировку.

На структурной схеме* апериодическое звено изображается так, как показано на рис. 6.18.

Интегрирующее звено. К интегрирующим звеньям относятся такие, у которых выходная величина связана с входной соотношением

вх = т . (6 26)

* Структурная схема автоматической системы регулирования представляет собой условную схему, на которой все элементы системы изображают в виде типовых динамических звеньев или их комбинаций и показывают все связи между этими звеньями (т. е. цепи передачи сигналов).