вательность единичных импульсов:

га [га - т, е - У = < К [\ е-Р ( - +e-f,)]

U*[l-*-p<n-M+e-4I, Y <e<I+F.,

(3.19)

где m = 0, 1,2 .., (га - 1).

С учетом выражений (3.15), (3.19) формулы для расчета тока в фазе ВДПМ примут вид

/[га, е] =

[ U (п)к[\-е~* £ (t/(m)[l-e-p < -fa+ - )]

- (7, (m)/( [l - <TP (e-+- )]}, < e < Y ; U(n)K[l -е~* (Е-?з)]- t7,(ra)/C[l -e-p(E-Y )] + + I {£/(m)/c[l e-<J(e- + - )]

-t71(m)[l-e-p+ -m)]}, v <e<I +?e,

(3.20)

<У (ra) = £/sign (sin шга) - <? [га] + e[ra - 1]; U(m) = U sign (sin am) - e[m] + e[m - 1]; У, (ra) = £/ sign (sin йга); (3-21)

Ux (m) = U sign (sin am).

Полученные выражения позволяют рассчитать кривую тока в фазе двигателя с учетом импульсного питания. Для расчета пульсационных потерь в меди обмотки ВДПМ необходимо кривую тока разложить в гармонический ряд. Так как длительность импульсов питающего напряжения изменяется в течение полупериода выходного сигнала ДПР, то разложение кривой тока в гармонический ряд с использованием значений тока в точках е = 13 и г=уп невозможно даже по приближенным формулам Бесселя [21]. Поэтому следует по формуле (3.20) определять значения t[ra, е] в равноотстоящих относительно друг друга точках в пределах периода Т и использовать их для нахождения коэффициентов гармонического ряда. Число точек деления будет определяться наибольшим номером интересующей нас гармоники. Обозначим через F число тактовых интервалов в периоде выходного сигнала ДПР. Тогда коэффициенты гармони-

где

ческого ряда найдутся по формулам Бесселя:

sF -l

k = 0

2kni\n sFn

2kni\Ti sF

где mi = 1, 2, sFn/2; s - число точек деления периода Т.

Ток в фазе двигателя запишется в виде

£ / cos (т,а>/- <р),

где lm = \Jam + bim;

l bm , , sFn Ф = агс1ё-; г, < -

Для нахождения мощности, потребляемой от источника постоянного напряжения на интервале коммутации, проинтегрируем ток на участке [3, уп]:

1 п

р (n) = U sign (sin era) i(t)di.

Непосредственное использование формулы (3.20) приводит к весьма громоздким выражениям. Поэтому для расчета потребляемой мощности положим изменение тока в пределах каждого из s участков деления периода тактовой частоты линейным. Это допущение правомерно, так как в схемах с ШИМ обычно электромагнитная постоянная силовой цепи значительно больше Т. Тогда выражение для потребляемой мощности будет иметь вид

ч 1 ( I \ i[n, уп

P(n) = U sign (sin an) < [уп - -)-

, +L 2s у

] + l [n, ei]

где i[n, 8s []s=,i = / [ra, t3]; I - число точек деления периода Т, попадающих в интервал []3, уп].

Мощность, потребляемая фазой двигателя в установившемся режиме, определим как сумму

л,.ф=т- I р(п).

Потери в меди фазы ВДПМ и электромагнитный КПД:

Eh cos(9 + ср).

- Р

2 9М'

г| = Рэм/(2Рп.ф),

3.5. Энергетические характеристики ВДПМ

Анализ энергетических характеристик ВДПМ существенно упростится, если перейти к системе относительных единиц. За базовые примем те же величины, что и в § 3.2.

Кроме того, введем обозначение $\-Тх/Тэ-отношение периода выходного напряжения ДПР к постоянной времени силовой цепи двигателя. Необходимость введения переменной $\ обусловлена тем, что с изменением F величина р при неизменных параметрах силовой цепи изменяется. Поэтому выявить влияние, например, частоты коммутации на энергетические характеристики ВДПМ трудно, хотя традиционно в литературе принимается за независимую переменную величина (3 [22]. В данном случае при фиксированной частоте вращения величина Pi не зависит от частоты коммутации. Заметим, что ш = 2k/F ;

(3 = Pl/Fn.

Тогда выражения для расчета тока в относительных единицах примут вид

i [п, е] =

и(п)\\-е f J + 2 ,1и(т)\\-е F )-

- щ (m)\\- e J], r3<e<v ;

u(n)\l-e J-u{(n)\l-e F J+ A1 [ ( -а.

- щ(т)\\-е )\, y

(3.22)

где

<?[ ], e[mj-относительные значения средней ЭДС вращения на соответствующих периодах напряжения ШИМ. Мощность, потребляемая фазой двигателя,

Р 2 П+РП2 2 f /

s-l - 4

ч/ < [n, уя] + г ei] г [rc, e5] + i [n, e -,] ( (3 23)

s-l J

Электромагнитная мощность

Рэм = v/j cos (ф + Э), <

где7[=/, баз.

Оптимальное значение угла Э, выраженное через относительные единицы,

v 6, , 2я

1 Qt-+iT -.

9 = arcsin -===!===- - arctg

л/1 + (2я/й,)2 р,

л/1+(2я/й,)2 Pi

Таким образом, при фиксированной частоте вращения вала v варьируемыми величинами при исследовании влияния параметров и частоты коммутации на энергетические характеристики

ВДПМ являются Fn, Pj и t3.

Добавочные потери в меди обмоток двигателя рДОб, обусловленные импульсным питанием, могут быть определены путем сравнения мощности р„. ф [см. выражение (3.23)], потребляемой от источника с ШИМ, с мощностью р ф, потребляемой от источника синусоидального напряжения (в относительных единицах) :

Рдоб = Рп. ф - Р~Ф (3-24)

При этом электромагнитная мощность, развиваемая в двигателе, в том и другом случае должна быть одинаковой. Тогда справедливо равенство

Рм.ф = Рм1ф. (3-25)

где р„. ф - относительные потери в меди фазы при питании от источника синусоидального напряжения; рМ]ф - относительные потери в меди фазы от первой грамоники тока в случае позиционной модуляции.

Поскольку рп ф = рм1ф + рдоб + j рЭ!Л И Р„ф = Р№.ф + Рэм, то с учетом выражений (3.24) и (3.25)

1

Рдоб Рп. ф Рм1ф 2 Рэм'

Снижение электромагнитного КПД ВДПМ при импульсном питании по сравнению с КПД двигателя при питании его от идеализированного источника синусоидального напряжения оценим как отношение

&ц - Лэм/ Лэм,

гДе Л,м = Рэы/(2п.ф); эмРэмЯ2 (Рп. ф - Рдоб)].

Величину кц примем как критерий оценки пульсационных потерь в ВДПМ.

При исследовании энергетических характеристик ВДПМ величина р( изменялась от f5i = 3 до pi = 18, что охватывает широкий диапазон изменения параметров силовой цепи. Выбор значений F осуществляется из следующих соображений. Известно [23, 24], что для синусоидальной позиционной модуляции при F < 10 зависимость фазы и амплитуды основной гармоники напряжения от фазы и амплитуды модулирующего сигнала существенно нелинейна. Кроме того, при малых Fn амплитуда и фаза основной гармоники напряжения ШИМ зависят от начальной фазы первого импульса тактовой

> 5)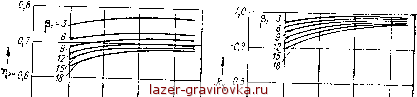

0,5)-

22 2S

/4 Fn

Рис. 3.7. К расчету энергетических показателей ВДПМ

частоты в периоде модулирующего сигнала. В итоге эта зависимость приводит к возникновению модуляции частоты вращения вала двигателя пониженной частотой. С увеличением F (Fn 10) амплитуда основной гармоники не зависит от фазы модулирующего сигнала, а фазовая характеристика становится линейной. Поэтому для синусоидального закона позиционной модуляции величина Fn задавалась, начиная с Fn = 10. По тем же соображениям для трапецеидального закона позиционной модуляции рассматривались значения Fu 12.

На рис. 3.7, а, б приведены кривые зависимостей соответственно r),M(F ) и kn (Fn) для синусоидального закона позиционной модуляции, пользуясь которыми, можно определить степень ухудшения КПД двигателя в случае позиционной модуляции по сравнению с питанием от идеализированного источника синусоидального напряжения. При этом рассматривался режим работы ВДПМ на естественной механической характеристике вблизи максимума КПД (v = 0,7). С увеличением частоты коммутации начиная с F = = 18 ... 22 (в зависимости от величины Pi) практически не наблюдается роста КПД и k, в то время как при F < 18 наблюдается снижение КПД из-за увеличения содержания высших гармоник в кривой фазного тока, которое составляет 2 % для F = 10 при р\ = 6 и 6 % при р\ = 18. С ростом относительной частоты вращения снижение КПД при F < 18 более существенно и, например, для v = 0,9 составляет 5 % при {$t = 6 и 18 % при

Pi = 18. Это обусловлено ростом удельного веса потерь от высших гармоник с частотой коммутации по отношению к основной гармонике тока.

Аналогичные расчеты для трапецеидальной и дискретной 120-градусной коммутации позволяют сравнить энергетические показатели соответствующих ВД. На рис. 3.8 приведены кривые зависимостей vjэм (рt), соответствующие Fn 22, для синусоидального (/), трапецеидального (2) закона позиционной модуляции и дискретной коммутации (<?), откуда следует преимущество синусоидальной позиционной модуляции по уровню электромагнитного КПД. Это преимущество сохраняется и при остальных значениях относительной частоты вращения v во всем диапазоне изменения параметров силовой цепи.

На уровень коэффициента полезного действия ВДПМ влияют также потери в силовых ключах коммутатора. В режиме переключений потери в транзисторах складываются из следующих составляющих:

V 0,6

ЛРт = ЛРотс + АРнас + ДЛ

Рис. 3.8. Кривые коэффициента полезного действия ВДПМ при v = 0,7 для си-пер, нусоидального (7), трапецеидального (2) закона позиционной модуляции и дискретной коммутации (3)

где АРотс - потери в режиме отсечки; АРнас - потери в режиме насыщения; АРпер - мощность, рассеиваемая транзистором при переключении, - динамические потери.

Величиной АРотс обычно пренебрегают. Потери APHac учитываются при расчете потерь в активном сопротивлении силовой цепи двигателя соответствующим его увеличением. Как показано в работе [25], потери при переключениях АР ер в основном равны потерям в активной области, т. е.

пер

АРЯ

(3.26)

где /+, /- - ток через транзистор в момент его включения и выключения соответственно; t+, t~-время включения и выключения транзистора; ]\ - частота переключений.

Поскольку транзисторы инвертора коммутируют ток, изменяющийся от импульса к импульсу, то степень их насыщения и длительность фронтов коллекторного тока также изменяются. Выражения для расчета t+ и t~ имеют вид [3]

t+ = tr In

Р l-+/(Wi) I (3.27)

r = Tftln[l + /7(/maxS;)].J

где Tp - постоянная времени переходной характеристики коэф-